天干地支纪年法与最小公倍数

缘由

最近在读西游记，看到西游记第一回，第一页便提到了12地支，联想到10天干，于是把天干地支纪年法是怎么回事琢磨了下，详见下文。

正文

我国早期采用天干地支纪年法。

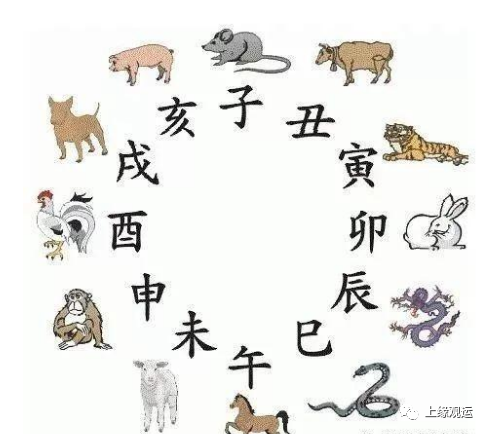
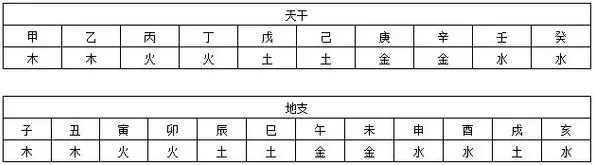
10天干为：甲、乙、丙、丁、戊、己、庚、辛、壬、癸。

12地支为：子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥。

天干地支纪年法的规则为：第一列为天干、第二列为地支，天干与地支的每一个组合代表一年。需要注意的是：10天干竖向出现完成一轮后，继续按照10天干的顺序循环出现；同样，12地支竖向出现完成后一轮后，继续按照12地支的顺序循环出现。（具体排列见下文插图）

那么问题来了，天干地支一个循环需要多少年？该问题等价于天干地支循环的最后一个组合第几年出现？

具体而言，天干地支循环第一个组合为“甲子”年，那么天干地支循环的最后一个组合是什么年？

第二个“甲子”年的上一个是组合是什么年？

天干地支循环的最后一个组合为10天干的最后一个字“癸”与12地支的最后一个字“亥”，即“癸亥”。

只有当“癸亥”出现后，才会第二次出现“甲子”。

天干地支循环的最后一个组合是“癸亥”，“癸亥”第几年出现呢？

当然，使用excel，按照上述规则进行排列（见下图），会发现第2次出现甲子年是第61年，天干地支循环的最后一个组合“癸亥”第一次出现是在第60年。这就是60一甲子的来历。

一个天干地支纪年法循环的排列

那么，除了一个个排列，能否使用数学工具解决该问题呢？

天干地支循环的最后一个组合是“癸亥”，“癸亥”第几年出现呢？

在10天干的循环排列中，“癸”只在第10，20，30，40，50，60，70，80等10的倍数年才出现；在12地支中，“亥”只在第12，24，36，48，60，72等12的倍数年才出现。从举例中发现，“癸”与“亥”同时在第60年出现。

只有“癸”与“亥”的出场顺序相同时，“癸”与“亥”才会相遇；第一次相遇的时间即为10与12的最小公倍数。

两个数字的最小公倍数=两个数字的乘积/两个数字的最大公约数。

10=2*5

12=2*6，12=3*4

10与12的最大公约数为2。

故10与12的最小公倍数=10*12/2=60。

题外话

话说，按照干支纪年法，今年是什么年？明年呢？